
Kahn (1967) describes instances of lovers engaging in secret communications enciphered using the Caesar cipher in The Times. In the 19th century, the personal advertisements section in newspapers would sometimes be used to exchange messages encrypted using simple cipher schemes. The earliest surviving records date to the 9th century in the Arab world with the discovery of frequency analysis. Assuming that an attacker could read the message, there is no record at that time of any techniques for the solution of simple substitution ciphers.
It is unknown how effective the Caesar cipher was at the time, but it is likely to have been reasonably secure, not least because few of Caesar's enemies would have been literate, let alone able to consider cryptanalysis. There is evidence that Julius Caesar used more complicated systems as well, and one writer, Aulus Gellius, refers to a (now lost) treatise on his ciphers: There is even a rather ingeniously written treatise by the grammarian Probus concerning the secret meaning of letters in the composition of Caesar's epistles. Julius Caesar's nephew Augustus also used the cipher, but with a shift of one: Whenever he wrote in cipher, he wrote B for A, C for B, and the rest of the letters on the same principle, using AA for X. While Caesar's was the first recorded use of this scheme, other substitution ciphers are known to have been used earlier. If anyone wishes to decipher these, and get at their meaning, he must substitute the fourth letter of the alphabet, namely D, for A, and so with the others. The Caesar cipher is named after Julius Caesar, who, according to Suetonius, used it with a shift of three to protect messages of military significance: If he had anything confidential to say, he wrote it in cipher, that is, by so changing the order of the letters of the alphabet, that not a word could be made out. The Caesar cipher is named for Julius Caesar, who used an alphabet with a shift of three. The replacement remains the same throughout the message, so the cipher is classed as a type of monoalphabetic substitution, as opposed to polyalphabetic substitution. Encryption of a letter x by a shift n can be described mathematically as, The encryption can also be represented using modular arithmetic by first transforming the letters into numbers, according to the scheme, A = 0, B = 1., Z = 25. Plaintext: the quick brown fox jumps over the lazy dog Ciphertext: WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ To encipher a message, simply look up each letter of the message in the "plain" line and write down the corresponding letter in the "cipher" line. For instance, here is a Caesar cipher using a right rotation of three places (the shift parameter, here 3, is used as the key): Plain: abcdefghijklmnopqrstuvwxyz Cipher: DEFGHIJKLMNOPQRSTUVWXYZABC The transformation can be represented by aligning two alphabets the cipher alphabet is the plain alphabet rotated left or right by some number of positions. As with all single alphabet substitution ciphers, the Caesar cipher is easily broken and in practice offers essentially no communication security. The encryption step performed by a Caesar cipher is often incorporated as part of more complex schemes, such as the Vigenère cipher, and still has modern application in the ROT13 system.

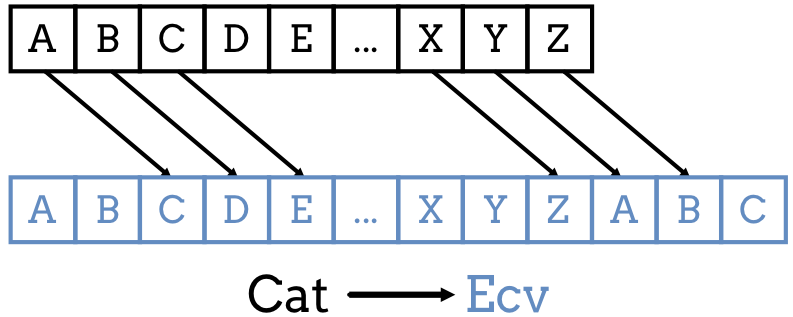
The method is named after Julius Caesar, who used it to communicate with his generals. For example, with a shift of 3, A would be replaced by D, B would become E, and so on.

It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions further down the alphabet.
SHIFT CIPHER DECODER CODE
In cryptography, a Caesar cipher, also known as a Caesar's cipher, the shift cipher, Caesar's Code or Caesar Shift, is one of the simplest and most widely-known encryption techniques. This example is with a shift of three, so that a B in the plaintext becomes E in the ciphertext. The action of a Caesar cipher is to replace each plaintext letter with one a fixed number of places down the alphabet.


 0 kommentar(er)
0 kommentar(er)
